Show That an Equation Has Exactly One Root
The objective is to prove that the given equation has exactly one real root. For the equation x 2a1x2a0 to have exactly one root lying between the interval 03 the following conditions should be satisfied i f0f3.

Rolle S Theorem To Prove Exactly One Root For Cubic Function Ap Calculus Youtube
Okay Now we are being asked to show that the equation has exactly one root.

. Now f 0 0 0 1 1 0. Using the intermediate value theorem there exists c in -1 1 such that f c 0. Lim x f x and lim x f x so the function has at least one real root.
The equation is x x cubed plus the F X equals zero. The objective is to prove that the given equation has exactly one real root. F x 2 sin.
And were trying to show were trying to prove that this. Solution for Show that the equation has exactly one real root. Get an answer for x3 ex 0 Show that the equation has exactly one real root and find homework help for other Math questions at eNotes.
Thus the given equation has at least one real root. Using the intermediate value theorem f is continuous and f o-1 and f 11 the equation has one root. Since f is the sum of a polynomial and the natural exponential function f is continuous.
Let f x x3 x 1. Answer 1 of 15. By Descartes rule of signs the polynomial function has 0 positive real roots and 1 negative real root.
2x cos x 0. F 1 1 1 1 1. Then we need to show that there exists a point where f is less than zero and a point where f is greater than zero.
Then f a0f b. Find step-by-step Calculus solutions and your answer to the following textbook question. Take two numbers say -1 and 0.
If the equation has distinct real roots a and. Get an answer for 2x cosx 0 Show that the equation has exactly one real root and find homework help for other Math questions at eNotes. Then f -1 -6 0 and f 0 1 0 Letting f x 1 2x x3 4x5 By the Intermediate Value Theorem there.
To show that there is exactly 1 real root we start with the IVT to show that roots exist. X Notice that f x 0 for all values of x. Show that the equation has exactly one real root.
Since f is continuous on a b and differentiable on a b. Then -1 0 and o 0. Step 1 of 4.
Answered Nov 26 2019 by SumanMandal 547k points selected Nov 26 2019 by Raghab. X e 0 3. This shows that f x has a root.
B with a b then f a f b 0. Show that the equation has exactly one real root. To show that the function has only one real root we have to show that it is monotonic in.
I would show that the given function fxx33x1 has no turning points then couple this with the fact that any odd powered polynomial will have at least 1 real answer. Since 0 is not a root there is exactly one real root. Then we use a very common math technique which is proof by contradiction.
Supposing it has two roots a and b and. My Limits Continuity course. Nov 20 2008.
Then we need to show that there exists a point where f is less than zero and. X5 ex 0 Let f x x5 eX.

Rolle S Theorem To Prove Exactly One Root For Cubic Function Ap Calculus Youtube

Rolle S Theorem To Prove Exactly One Root For Cubic Function Ap Calculus Youtube
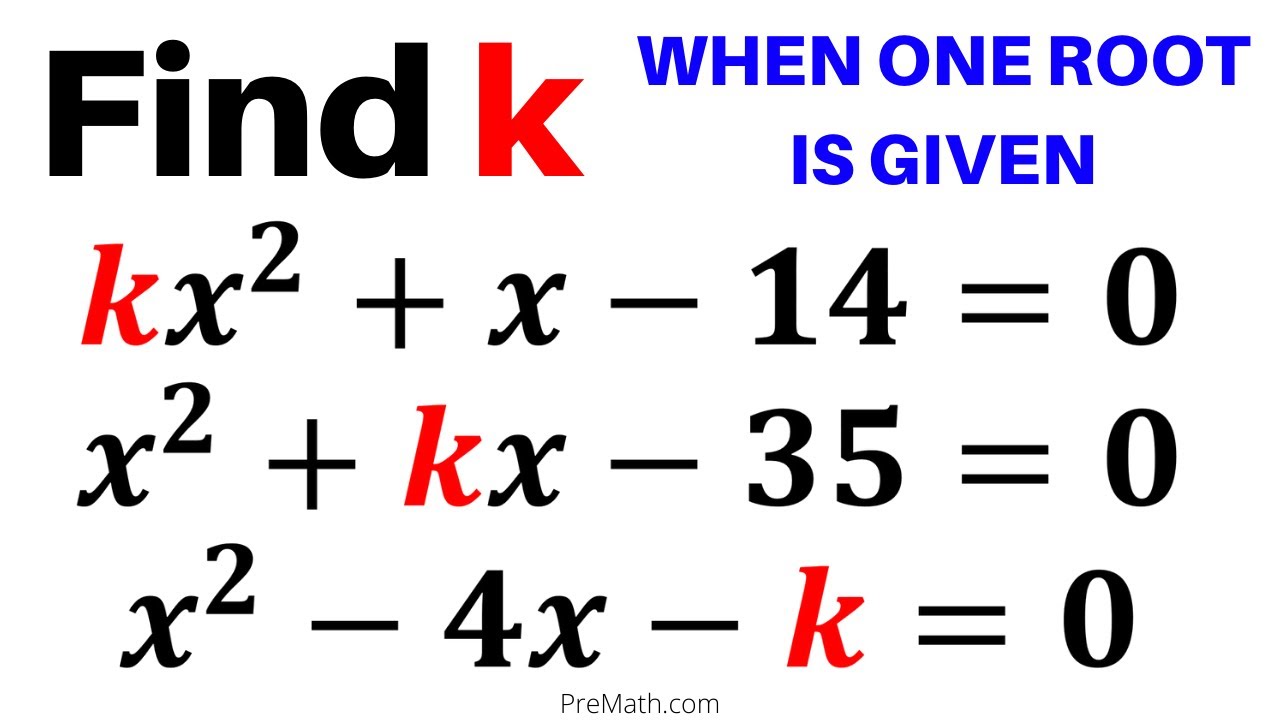
Find The Value Of K In Quadratic Equations When One Root Is Given Step By Step Explanation Youtube
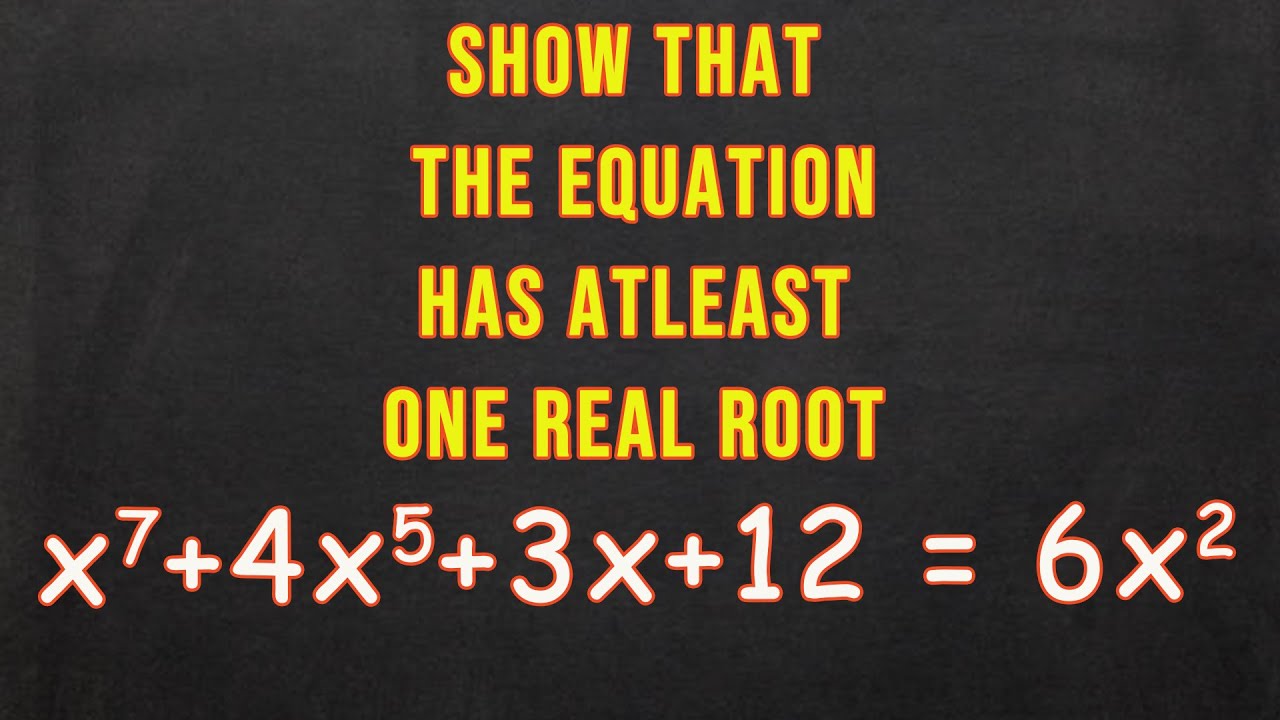
Comments
Post a Comment